Regardez l’image ci-dessous. Les nombres sont disposés selon une certaine règle. Une fois que vous avez trouvé la règle, complétez le nombre manquant. Le chiffre sept dans le dernier cercle n’est pas une erreur typographique.
Je trouve cette énigme irrésistible. Elle a l’air intrigante. Elle ne nécessite pas de mathématiques avancées. Il vous met au défi de le résoudre, et lorsque vous y parvenez (si vous y parvenez), le sentiment de satisfaction est à la fois exaltant et addictif. Nob Yoshigahara, célèbre inventeur de puzzles japonais du XXe siècle, le considérait comme son chef-d’œuvre. Essayez de trouver la réponse avant que je ne la révèle, En-dessous, comme d’habitude, en mode ‘caché’ (il est en blanc sur fond blanc, il faut passer la souris sur le texte pour le faire apparaître)
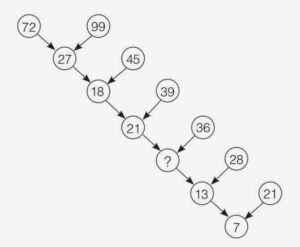
Solution :
Lorsque vous regardez l' »arbre des nombres », votre regard se porte sur le sommet à gauche. Comment 72 et 99 peuvent-ils faire 27 ?
Vous l’avez trouvé ! 99 – 72 = 27.
En d’autres termes, le nombre dans un cercle est la différence des nombres dans les deux cercles qui pointent vers lui.
Et regardez, le même schéma se répète avec 18, le nombre suivant :
45 – 27 = 18
Et avec 21 aussi : 3
9 – 18 = 21
Ce qui signifie que le nombre manquant doit être la différence entre 21 et 36, soit 15 :
36 – 21 = 15
Par souci d’exhaustivité, nous continuons à descendre dans l’arbre : 28 – 15 = 13
C’est bien ! Donc ça continue à fonctionner. On y est presque.
Jusqu’à ce que BOOM.
Le tout dernier chiffre est 7, qui n’est pas la différence entre 13 et 21, les deux chiffres qui le pointent.
Zut ! Notre hypothèse de départ est fausse. Il n’est pas vrai qu’un nombre dans un cercle est égal à la différence entre les deux nombres qui le pointent. Yoshigahara nous a habilement menés sur un chemin de traverse, pour nous faire trébucher au bout du chemin.
Retour à la case départ. Ou plutôt au premier cercle. Sinon, comment 72 et 99 peuvent-ils donner 27 ?
La réponse est si simple que vous l’avez peut-être manquée. 7 + 2 + 9 + 9 = 27
Les chiffres s’additionnent.
Et cela fonctionne pour la ligne suivante :
2 + 7 + 4 + 5 = 18
Et la suivante. Donc le nombre manquant doit être :
2 + 1 + 3 + 6 = 12
Les deux derniers cercles sont maintenant dans la même ligne :
1 + 2 + 2 + 8 = 13
1 + 3 + 2 + 1 = 7
L’énigme est fantastiquement ingénieuse parce que Yoshigahara a trouvé deux règles arithmétiques qui correspondent aux mêmes nombres pour cinq étapes de la séquence, mais dont une seule échoue pour l’étape finale, et seulement de 1. La facilité avec laquelle il nous met dans la mauvaise direction est magique.
Souvent, un problème est difficile non pas parce que c’est un « problème difficile », mais parce que nous nous y prenons de la mauvaise façon.


