L’histoire de Louis de Broglie est celle d’un prince devenu physicien, dont les travaux sur la nature de l’électron ont marqué l’histoire et contribué au développement de la mécanique quantique.
Il y a 100 ans, le 25 novembre 1924, le prince Louis Victor de Broglie (1892-1987), âgé de 32 ans, défendait sa thèse de doctorat en physique devant un jury comprenant Paul Langevin et Jean Perrin. Il y exposait sa théorie de la dualité onde-particule appliquée aux électrons.
Cinq ans plus tard, il recevra, à seulement 37 ans, le Prix Nobel de Physique pour sa « découverte de la nature ondulatoire de l’électron ».
Il sera élu en 1933 membre de l’Académie des sciences, puis en 1944 à l’Académie française, où il est accueilli par son propre frère Maurice. En 1960, Louis héritera du titre de duc à la mort de ce frère aîné. Quel fascinant parcours !
Le photon entre onde et corpuscule
Le monde de l’infiniment petit, celui des particules élémentaires, met en jeu des lois très éloignées de celles qui s’appliquent au monde ordinaire, en premier lieu la loi de gravitation strictement déterministe. Le comportement des particules est régi par une mécanique dite « quantique », qui a la particularité de ne prédire que des probabilités de réalisation d’un phénomène. On sait calculer précisément la trajectoire de la pierre qui tombe, cela n’est plus vrai pour une particule.
La nature de la lumière avait été débattue depuis le XVIIe siècle entre la vision granulaire de Newton et celle ondulatoire de Huyghens. Au XIXe siècle, avec les équations de Maxwell, la messe semblait dite et la nature ondulatoire de la lumière avérée.
Mais en 1905, Einstein changea la donne en interprétant l’« effet photoélectrique », dans lequel une plaque métallique illuminée peut produire de l’électricité seulement si la lumière qu’il reçoit possède une fréquence suffisante. Pour expliquer ce phénomène, Einstein imagina la lumière composée d’un flux d’objets élémentaires qu’il appelle photons : l’effet s’interprétait comme une collision entre les électrons du métal et les photons de la lumière incidente. Une énergie minimum est nécessaire pour arracher les électrons de la plaque, ce que permettent les photons bleus, plus énergétiques que les photons rouges.
Cela rejoignait l’idée émise par Planck en 1900, qui, pour expliquer le rayonnement du corps noir, c’est-à-dire une cavité chauffée emplie de gaz, émit l’hypothèse que les échanges d’énergie se font par petites quantités bien déterminées qu’il appelle « quanta » (c’est-à-dire grains élémentaires), dont l’énergie vérifie la formule dite de Planck E = hf où E désigne l’énergie et f la fréquence et donc la couleur (h est un paramètre physique minuscule appelé constante de Planck).
À partir de cette spéculation de Max Planck, Niels Bohr conçut le modèle planétaire de l’atome, où les électrons tournent autour du noyau sur des orbites d’énergies fixes, comme les planètes autour du soleil.
Avec l’interprétation d’Einstein de l’effet photoélectrique, la « quantification de la lumière » (c’est-à-dire que la lumière est composée de « grains élémentaires », des particules) revenait avec force.
Alors, la lumière est-elle une onde ou un flux de particules ? Les deux, est la surprenante réponse. C’est la fameuse dualité onde-particule qui admet deux facettes de la réalité : la lumière interagit sous forme de photons (des particules), mais elle se propage sous forme d’onde.
Cela amène à des conséquences qui peuvent choquer le bon sens, remettant en cause le déterminisme. En particulier, Werner Heisenberg écrivit ses relations d’incertitude qui nous enseignent qu’il est impossible de connaître précisément à la fois la position et la vitesse d’une particule.
L’électron joue à la corde
L’apport de Broglie est d’avoir démontré que les électrons peuvent eux aussi se comporter comme une onde. Il étendit donc l’idée de dualité onde-particule au-delà du photon, proposant une symétrie entre toutes les particules. Cette symétrie n’était pas évidente car il y a une grande différence entre un photon de masse nulle et un électron de masse bien définie. La masse nulle du photon l’oblige à toujours se déplacer à la vitesse c = 300000 kilomètres par seconde. Pour le photon, la relation de quantification de Planck s’écrit E = hf. De Broglie généralise au cas d’une particule massive et propose que la longueur d’onde λ d’une particule de masse m voyageant à la vitesse v soit donnée par la formule : λ = h/mv.

En 1994, un timbre-poste rappela la publication de la formule de Broglie : lambda = h/mv.
Notons que cette longueur d’onde est infinitésimale pour un objet macroscopique : une balle de 200 grammes, animée d’une vitesse de 15 mètres par seconde, correspond à une longueur d’onde de 2 10-34 mètres (soit trente-trois 0 puis un 1 après la virgule) ! Mais pour un électron accéléré par une tension de 100 V, la longueur d’onde devient 10-10 mètres, c’est l’espacement entre des atomes dans un cristal et c’est donc en envoyant un faisceau d’électrons à travers un cristal qu’on peut espérer détecter un effet « d’onde d’électrons ». Davisson et Germer firent l’expérience correspondante et observèrent en 1927 des images d’interférences et de diffractions à partir d’électrons, comme on en observe avec des rayons X, validant ainsi l’hypothèse de Broglie.
Le modèle planétaire de l’atome selon de Broglie
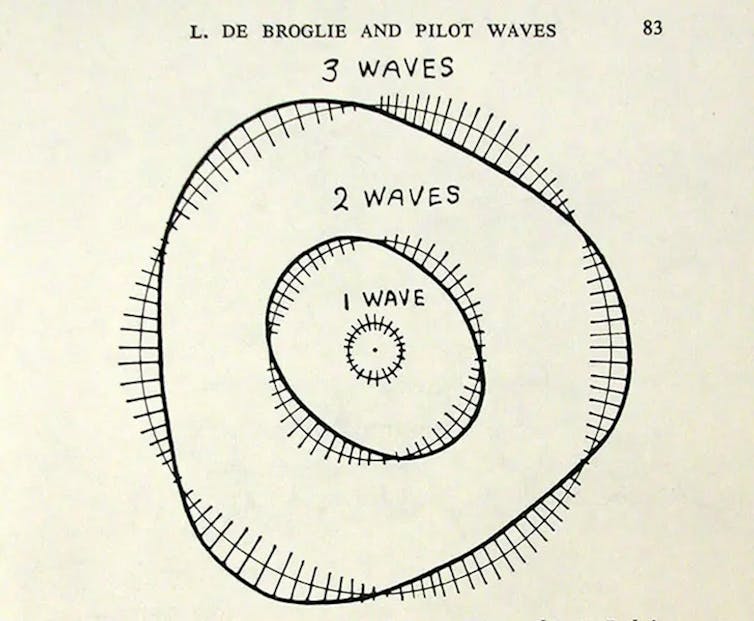
Les électrons de l’atome tournent autour du noyau selon des orbites « quantifiées » c’est-à-dire d’énergies fixes, et dans sa thèse, de Broglie expliquait cette propriété à partir du caractère ondulatoire de l’électron. Un raisonnement géométrique simple était développé : les électrons orbitent autour du noyau de l’atome selon des ondes stationnaires.
Quand la corde d’un violon est attaquée par l’archet, de nombreuses ondes sont engendrées, mais seules subsistent celles ayant des nœuds aux extrémités, ce sont les « modes résonnants » qui donnent les notes musicales. Par analogie, de Broglie imagine les électrons se déplaçant sur des cercles autour du noyau, les orbites doivent alors correspondre à des ondes stationnaires circulaires qui se referment sur elles-mêmes, comme la corde de violon dont les extrémités se toucheraient.
Le modèle de l’atome de Bohr, avec les éléctrons selon de Broglie. Dessin de George Gamow dans son livre « Thirty Years that Shook Physics », publié en 1966
Ainsi, pour une orbite de rayon R, la circonférence doit être un multiple de la longueur d’onde associée à l’électron, ce qui donne la relation : 2πR = nλ, n étant un entier prenant des valeurs 1,2,3… selon les différentes orbites.
Avec λ = h/mv, on obtient la condition d’une orbite stable : mvR = nh/2π. C’est ce qu’avait postulé Bohr. La dualité onde-particule explique donc bien la structure planétaire de l’atome. En pratique, le modèle est bien vérifié pour un atome ayant un électron, c’est-à-dire le cas de l’hydrogène, mais il est déficient pour un cas plus compliqué.
Il faudra imaginer une théorie totalement nouvelle, la mécanique quantique, développée avec force en particulier à Copenhague par Niels Bohr et ses élèves pour comprendre la structure atomique, et alors la vision de la réalité devint beaucoup plus complexe : les orbites ne sont plus des cercles définis mais des nuages d’électrons dont la probabilité de présence en chaque point de l’espace est donnée par une « fonction d’onde » qui vérifie l’équation d’évolution de Schrödinger.
Mécanique ondulatoire vs mécanique quantique
Aujourd’hui, la théorie ondulatoire de Broglie semble une ébauche à côté de la mécanique quantique qui signe une véritable révolution de la pensée. De Broglie restait dans le cadre ancien (quoi de plus classique qu’une corde ?). Il ne participa pas vraiment aux développements quantiques.
Déjà au Congrès Solvay, organisé en octobre 1927 sur le thème « Électrons et photons » à l’Institut de physique Solvay dans le parc Léopold de Bruxelles, de Broglie se retrouve au milieu des ténors de la mécanique quantique venus en force autour de leur pape, Niels Bohr. Ehrenfest, Schrödinger, Pauli, Heisenberg, Debye, Bragg, Kramers, Dirac, Compton, Born, Planck, Lorentz, sont présents — tous ou presque déjà ou bientôt Prix Nobel.

Le congrès de Solvay en 1927 rassembla les ténors de la physique quantique, dont Louis de Broglie, assis au deuxième rang – c’est le troisième en partant de la droite. DLR_next, Flickr
La mécanique quantique révéla des aspects de la réalité très surprenante : l’antimatière existe, la réalité n’est plus déterministe mais probabiliste, l’état d’un système n’est plus décrit par des positions et des vitesses mais par des fonctions d’onde, le hasard est une propriété intrinsèque de la matière…
Comme Einstein qui passa les dernières années de sa vie dans son repaire de Princeton, refusait le nouveau concept de réalité donné par la mécanique quantique et chercha en vain le Graal d’une « théorie du champ unifié » espérant relier l’électrodynamique à la gravitation, de Broglie tenta de prolonger ses idées de mécanique ondulatoire en une « thermodynamique cachée des particules » (Comptes rendus de l’Académie des sciences, 1963) qui ne déboucha sur rien de concret. Ses dernières années furent malheureuses. Perdant la mémoire, il vécut totalement dépendant et il mourut oublié du public et de ses collègues.
Quand on possède un glorieux pédigrée héraldique comme Louis de Broglie, il est difficile de sortir du rang et s’affirmer personnellement, un duc n’est qu’un numéro presque anonyme dans une suite de successions. Il faut devenir, à l’exemple de l’électron, un être dual et s’affranchir de son milieu pour s’illustrer individuellement. Proust, qui connaissait bien le monde de l’aristocratie, fait dans son œuvre maîtresse une allusion à un prince qui transcende son milieu d’origine en devenant docteur en physique (ou fameux politicien). Je ne peux m’empêcher de penser qu’il avait en tête le prince et physicien Louis de Broglie, dont il devait connaître la famille, à moins que ce ne soit le frère Maurice, lui aussi physicien. Ainsi la formule λ=h/mv a probablement fait entrer notre prince dans le casting de À la Recherche du temps perdu, ce qui, pour certains, est une reconnaissance aussi notoire que celle venant du comité Nobel.![]()
François Vannucci, Professeur émérite, chercheur en physique des particules, spécialiste des neutrinos, Université Paris Cité


