Si vous avez déjà entendu parler d’Einstein, il est fort probable que vous connaissez au moins une de ses équations parmi les plus fameuses : E=mc².
Cette équation, l’une des lus simples (et plus célèbres) de la physique met en relation l’énergie (E) d’un système,sa masse au repos (m) et le carré de la vitesse de la lumière dans le vide (c²) qui relie les deux.
On ne soupçonne généralement pas que cette équation, d’apparence si simple, a des conséquences dans notre vie de tous les jours.
Voici 5 leçons que chacun devrait en retenir :
1) La masse n’est pas conservée
Dans la vie de tous les jours, si vous découpez un objet en petits morceaux, la masse du corps et la masse totale des morceaux est la même, en tout cas, c’est ce à quoi on s’attend . Mais si on prend un atome, sa masse est différente de la somme des masses de ses éléments constitutifs (neutrons, protons et électrons) ; la différence est la quantité d’énergie nécessaire pour les maintenir ensemble …
2) L’énergie est conservée, mais seulement si on tient compte de la variation des masses.
Que ce soit dans un atome, une molécule ou un ion, les transitions d’électrons d’un niveau d’énergie supérieur à un niveau d’énergie inférieur entraîneront l’émission de rayonnement à une longueur d’onde très particulière. Cela produit le phénomène que nous voyons comme des lignes d’émission, et est responsable de la variété de couleurs que nous voyons dans un feu d’artifice. Même les transitions atomiques de ce type doivent conserver l’énergie, ce qui signifie perdre de la masse dans la bonne proportion pour tenir compte de l’énergie du photon produit.

3) L’équation E = mc² d’Einstein explique pourquoi le Soleil (comme toute étoile) brille.
Au cœur de notre Soleil, où les températures s’élèvent au-dessus d’une température critique de 4 000 000 K (jusqu’à près de quatre fois plus grande), les réactions nucléaires qui alimentent notre étoile ont lieu. Les protons fusionnent ensemble dans des conditions si extrêmes qu’ils peuvent former un deutéron – un état lié d’un proton et d’un neutron – tout en émettant un positron et un neutrino pour conserver leur énergie.
D’autres protons et deutérons peuvent alors bombarder la particule nouvellement formée, fusionnant ces noyaux dans une réaction en chaîne jusqu’à ce que l’hélium-4, avec deux protons et deux neutrons, soit créé.
Si l’on mettait ce produit final de l’hélium-4 sur une balance et qu’on le comparait aux quatre protons qui ont servi à le créer, on constaterait qu’il est environ 0,7% plus léger : l’hélium-4 ne contient que 99,3% de la masse des quatre protons. Même si deux de ces protons se sont transformés en neutrons, l’énergie de liaison est si forte qu’environ 28 MeV d’énergie est émise dans le processus de formation de chaque noyau d’hélium-4.
4) La conversion de la masse en énergie est le processus le plus énergétiquement efficace de l’Univers.
Si vous regardez l’équation E = mc2, elle vous dit que vous pouvez convertir la masse en énergie pure, et vous dit combien d’énergie vous en tirerez. Pour chaque kilogramme de masse que vous convertissez, vous obtenez un impressionnant 9 × 1016 joules d’énergie : l’équivalent de 21 Mégatonnes de TNT. Chaque fois que nous assistons à une désintégration radioactive, à une réaction de fission ou de fusion, ou à un événement d’annihilation entre la matière et l’antimatière, la masse des réactifs est plus grande que la masse des produits ; la différence est la quantité d’énergie qui est libérée.
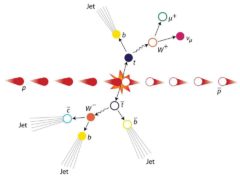
Dans tous les cas, l’énergie qui en résulte – sous toutes ses formes combinées – est exactement égale à l’équivalent énergétique de la perte de masse entre produits et réactifs.
5) Il est possible d’utiliser de l’énergie pour créer de la matière – des particules massives – à partir de rien d’autre que de l’énergie pure.
C’est peut-être la leçon la plus profonde de toutes. Si vous prenez deux boules de billard et que vous les lancez à grande vitesse l’une contre l’autre, vous vous attendez toujours à ce que les résultats aient quelque chose en commun : ils donnent toujours deux boules de billard et seulement deux.
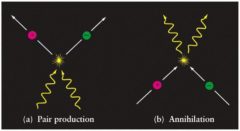
Avec les particules, cependant, l’histoire est différente. Si vous prenez deux électrons et que vous provoquez leur collision, vous obtiendrez deux électrons, mais avec assez d’énergie, vous pourriez aussi obtenir une nouvelle paire de particules de matière-antimatière aussi. En d’autres termes, vous aurez créé deux nouvelles particules massives là où il n’en existait aucune auparavant : une particule de matière (électron, muon, proton, etc.) et une particule d’antimatière (positron, anti-muon, antiproton, etc.).
Source (pour plus de détails et explications – en anglais) : Forbes


